报告题目：Efficient energy harvesting/extraction from ambient vibration
报告时间：2025年9月11日（星期四）14:00—15:00
报告地点：机械馆J3
报告人：Marian Wiercigroch（英国阿伯丁大学）
报告人简介：
Marian Wiercigroch教授是国际著名非线性动力学专家、英国爱丁堡皇家学会院士(Fellow)、波兰科学院技术科学部委员、英国机械工程师协会会士(Fellow)、英国数学与应用协会理事会成员、英国数学与应用协会会士(Fellow)、英国工程与自然科学研究理事会成员、英国阿伯丁大学“六世纪主席”教授、英国阿伯丁大学应用动力学研究中心主任、International Journal of Mechanical Sciences杂志主编（中科院工程技术大类1区TOP, IF=9.41），以及二十多本杂志编委及中国力学学报海外编委。同时也被英国阿伯丁大学及波兰罗茨科技大学授予荣誉博士，燕山大学外聘院士、浙江大学荣誉教授、哈尔滨工程大学讲座教授、宁波诺丁汉大学荣誉教授、俄罗斯彼尔姆国立研究理工大学荣誉教授，美国罗格斯大学极端环境结构研究中心特聘顾问教授、阿根廷巴尔塞罗研究所特及巴里洛切原子能研究中心特聘教授。Wiercigroch教授出版专著3本，参编15本著作、发表论文近600篇，常年担任世界各类力学会议主席、分会主席及会议理事会成员；发起或组织数十场国际学术会议。据Google Scholar，论文总引用数逾12988次，h-index为64。他的主要研究方向包括：非线性动力学与控制，具体研究包括：钻探、再生能源、金属切削，转子系统、水声学、疲劳等。
报告内容简介：
从环境振动中高效提取（或收集）能量依赖于将振荡运动有效转化为以电能为主的能量形式。压电材料因结构简单且高效而被广泛采用，其在机械应变时会产生电能。电磁与静电方法亦被应用，通过利用相对运动或电容变化来产生电能。为提高效率，通常采用共振调谐技术使器件的固有频率与环境振动频率匹配，从而实现能量捕获的最大化。能量收集电路可进一步优化转换过程，并将提取的能量存储以供后续使用。这种方法对于为偏远或难以抵达区域的传感器等低能耗设备供电具有重要价值。
Williams和Yates的开创性论文[1]提出了振动驱动微型发电机的分析模型，重点关注电磁转换机制。他们通过集总参数激励模型模拟电能输出，为微尺度能量收集装置的后续发展奠定了基础。Roundy等人[2]在此基础上拓展了针对低强度环境振动的压电转换器研究，通过建模与实验证明压电材料可利用环境振动为无线传感器节点供电。
阿伯丁大学应用动力学中心（CADR）提出了一种新颖的能量提取方案：利用旋转响应替代存在停滞点且受静摩擦影响的振荡响应。该方案基于文献[3]提出的参数摆动态响应理论，随后引发了大量关于摆系统建模、实验与设计的研究。这些摆系统在旋转模式下能够收集大量电能，具体案例可参见[4,5]。图1展示了CADR研发的双摆系统：两个摆体安装于共同柔性基座上，承受简谐垂直激励。基座的水平和垂直位移（记为X和Y）与摆角位移（θ1和θ2）通过弹性基座和谐波激励产生耦合效应，其运动方程已在文献[4]中建立。
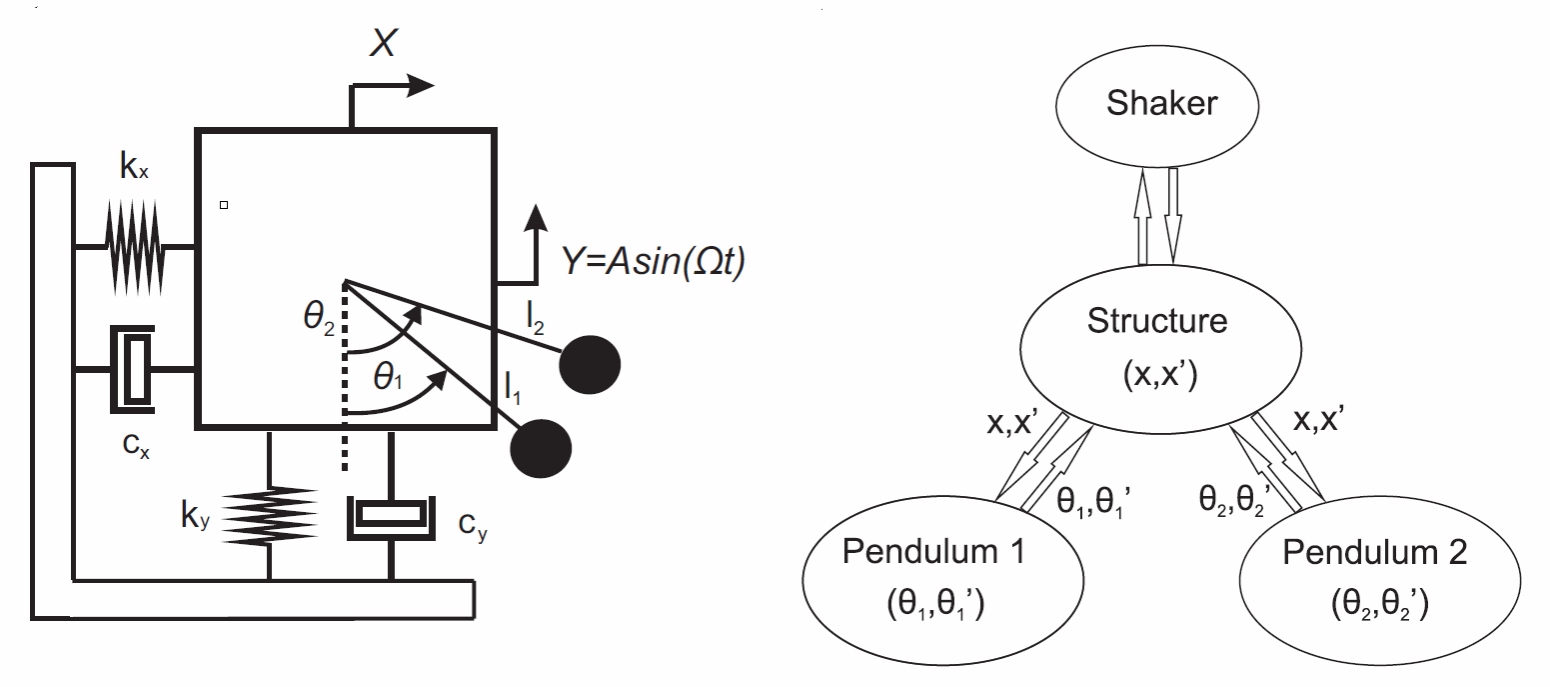
图1：双旋转摆系统；(a) 摆系统物理模型，(b) 结构与摆体相互作用示意图。引用自文献[3]
下文所示方程（1）和（2）为经过简化的无量纲运动方程，已被阿伯丁大学应用动力学中心（CADR）用于广泛的参数研究和稳定性分析，具体应用可参见文献[3-5]。
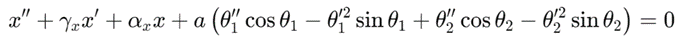
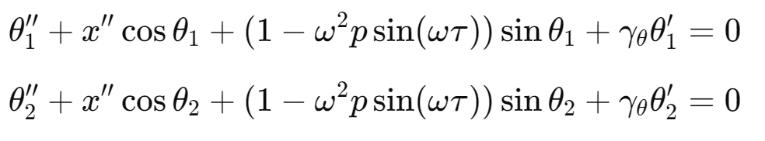
图2(a)-(c)展示了非线性动力学分析的代表性结果，其中子图(a)和(b)描绘了参数空间(ω,p)中经数值计算的鞍结分岔曲线。这些曲线对应两种刚度比条件下：双摆反向旋转（蓝色）、同向旋转（绿色）以及单摆旋转（红色）的旋转状态下限边界，具体参见文献[4]。理论研究结果已通过图2(d)所示摆系统实验得到验证。
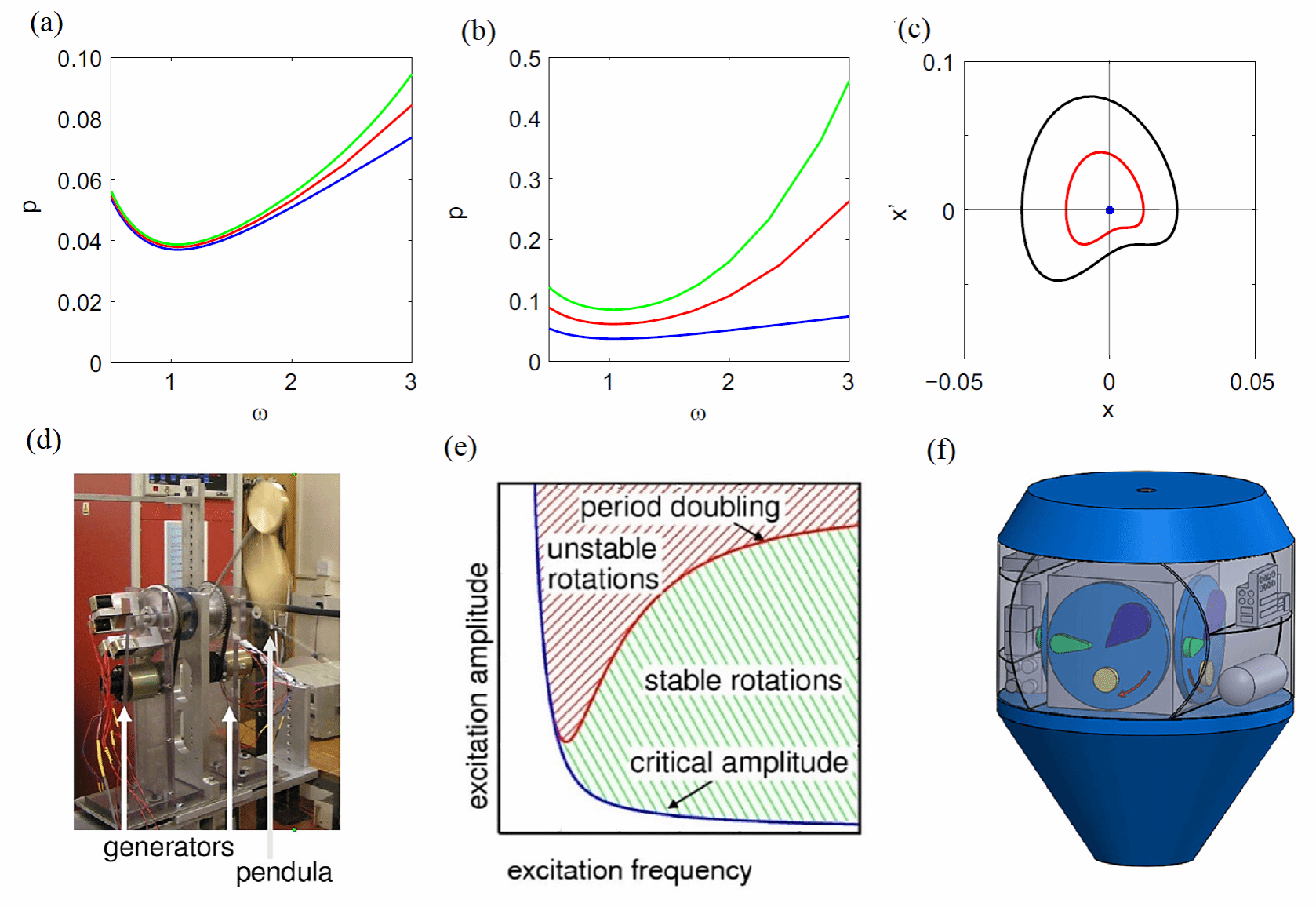
图2：反向旋转模式下摆系统的建模、实验与设计；
（a）和（b）参数稳定性图谱；
（c）基座振荡相图；
（d）实验装置；
（e）稳定性映射；
（f）搭载四对反向旋转摆的海洋浮标示意图。
根据CADR大量建模与实验研究可知，摆的旋转运动在能量提取效率和功率输出方面显著优于振荡运动。以参数摆为例：当频率和振幅设定为存在两个稳定吸引子（一个旋转吸引子，一个振荡吸引子）时，旋转模式提取的功率可达振荡模式的十倍[3]。这是因为旋转响应中的动能始终不为零，且不存在运动停滞点。
参考文献
[1] Williams C.B., Yates, R.B. (1996). Analysis of a micro-electric generator for microsystems. Sensors and Actuators A 52(1–3), 8–11.
[2] Roundy, S., Wright, P. K., Rabaey, J. (2003). A study of low level vibrations as a power source for wireless sensor nodes. Computer Communications, 26(11), 1131–1144.
[3] Xu X., Wiercigroch, M., Cartmell M.P. (2005). Rotating orbits of a parametrically excited pendulum. Chaos, Solitons & Fractals, 23(5), 1537–1548.
[4] Najdecka A., Kapitaniak T., Wiercigroch M. (2015) Rotational motion synchronization of parametric pendulums. International Journal of Non-linear Mechanics 70, 84-94.
[5] T Terrero González A., Dunning P., Howard I., McKee K., Wiercigroch M. (2021) Is wave energy untapped potential? International Journal of Mechanical Sciences 205, 106544.
